Học kỳ II lớp 9 là khoảng thời gian đầy thử thách với các em học sinh khi phải đối mặt với kỳ thi vào 10 đầy căng thẳng. Để giúp các em tự tin hơn trong hành trình chinh phục kỳ thi quan trọng này, bài viết này sẽ cung cấp cẩm nang đầy đủ về Công Thức Hình Học Lớp 9, một phần không thể thiếu trong đề thi.
 Hình học lớp 9 – Tam giác
Hình học lớp 9 – Tam giác
Hệ thống Công thức Hình học Lớp 9 – Nắm Chắc Kiến Thức
Chương 1: Hệ Thức Lượng Trong Tam Giác Vuông
- Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
- a² = b² + c² (với a là cạnh huyền, b và c là hai cạnh góc vuông).
- Hệ thức giữa cạnh góc vuông và hình chiếu:
- b² = a.b’ ; c² = a.c’ (với b’ và c’ lần lượt là hình chiếu của b và c lên cạnh huyền a).
- Hệ thức giữa đường cao và hình chiếu:
- h² = b’.c’ (với h là đường cao kẻ từ đỉnh góc vuông).
- Hệ thức giữa đường cao và cạnh huyền:
- 1/h² = 1/b² + 1/c²
- Hệ thức giữa đường cao và hai cạnh góc vuông:
- h = b.c/a
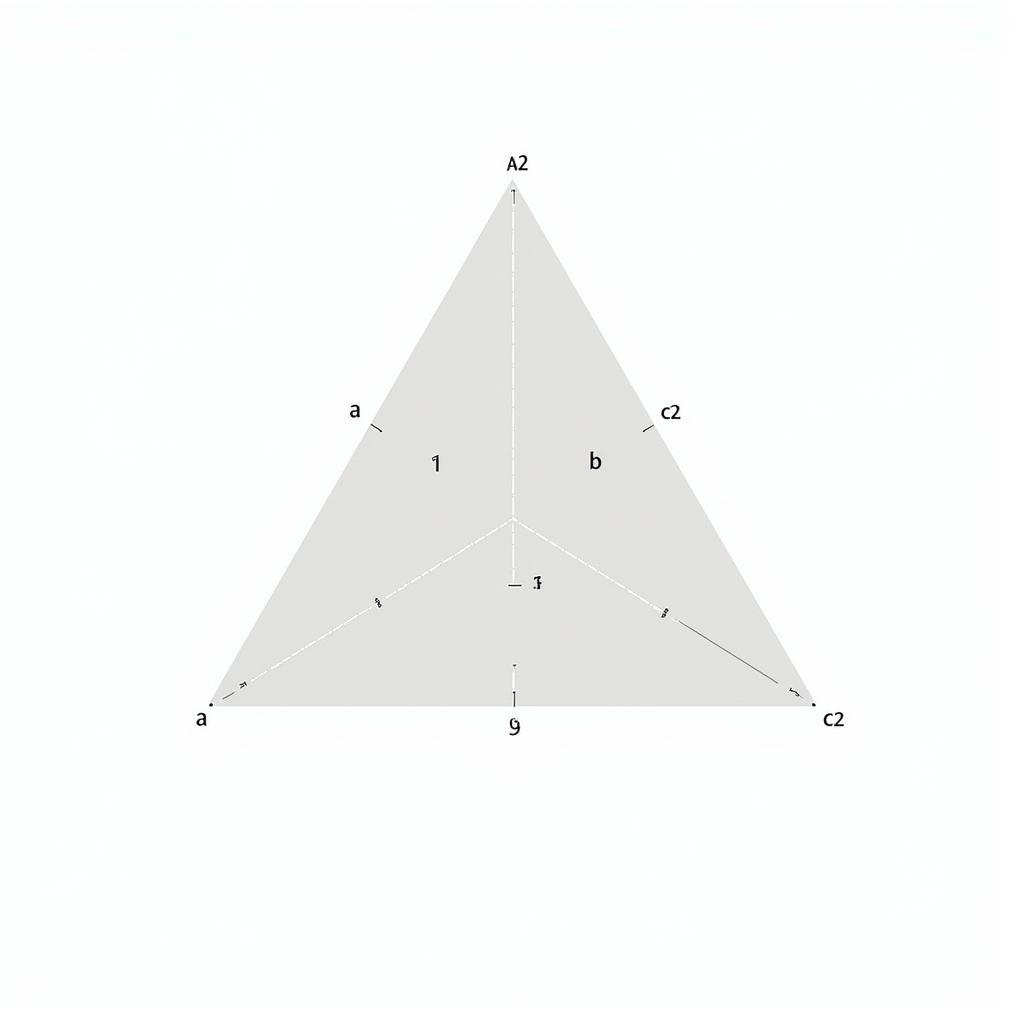 Minh họa định lý Pytago trong tam giác vuông
Minh họa định lý Pytago trong tam giác vuông
Chương 2: Đường Tròn
- Độ dài đường tròn:
- C = 2πR = πd (với R là bán kính, d là đường kính).
- Độ dài cung tròn n độ:
- l = πRn/180.
- Diện tích hình tròn:
- S = πR².
- Diện tích hình quạt tròn n độ:
- S = πR²n/360.
- Góc nội tiếp:
- Số đo góc nội tiếp bằng nửa số đo cung bị chắn.
- Góc tạo bởi tiếp tuyến và dây cung:
- Số đo góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.
- Hai góc nội tiếp cùng chắn một cung:
- Hai góc nội tiếp cùng chắn một cung thì bằng nhau.
- Tứ giác nội tiếp:
- Tứ giác có tổng hai góc đối bằng 180 độ là tứ giác nội tiếp.
- Tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện là tứ giác nội tiếp.
Chương 3: Góc Với Đường Tròn
- Góc ở tâm:
- Số đo góc ở tâm bằng số đo cung bị chắn.
- Góc nội tiếp:
- Số đo góc nội tiếp bằng nửa số đo góc ở tâm cùng chắn một cung.
- Góc tạo bởi tia tiếp tuyến và dây cung:
- Số đo góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.
- Góc có đỉnh nằm bên trong đường tròn:
- Số đo góc bằng nửa tổng số đo hai cung bị chắn.
- Góc có đỉnh nằm bên ngoài đường tròn:
- Số đo góc bằng nửa hiệu số đo hai cung bị chắn.
 Công thức tính diện tích hình tròn
Công thức tính diện tích hình tròn
Chương 4: Hình Học Không Gian
- Thể tích hình lăng trụ đứng:
- V = B.h (với B là diện tích đáy, h là chiều cao).
- Diện tích xung quanh hình lăng trụ đứng:
- Sxq = 2p.h (với p là nửa chu vi đáy, h là chiều cao).
- Diện tích toàn phần hình lăng trụ đứng:
- Stp = Sxq + 2.B
- Thể tích hình chóp đều:
- V = 1/3.B.h (với B là diện tích đáy, h là chiều cao).
- Diện tích xung quanh hình chóp đều:
- Sxq = 1/2.p.d (với p là nửa chu vi đáy, d là đường cao của mặt bên).
- Diện tích toàn phần hình chóp đều:
- Stp = Sxq + B.
Làm Chủ Công Thức Hình Học Lớp 9 – Bí Quyết Thành Công
Để học tốt và ghi nhớ công thức hình học lớp 9 một cách hiệu quả, các em học sinh có thể áp dụng những bí quyết sau:
- Học theo sơ đồ tư duy: Sử dụng sơ đồ tư duy để hệ thống các công thức theo từng chủ đề, giúp dễ nhớ và dễ dàng hình dung mối liên hệ giữa chúng.
- Luyện tập thường xuyên: Luyện giải các bài tập từ cơ bản đến nâng cao để thành thạo trong việc áp dụng công thức vào giải toán.
- Ôn tập và luyện đề: Ôn tập thường xuyên và luyện giải đề thi các năm trước để rèn luyện kỹ năng làm bài và quen với dạng bài trong phòng thi.
- Tự tin và bình tĩnh: Giữ tinh thần thoải mái, tự tin và bình tĩnh khi bước vào phòng thi để đạt kết quả cao nhất.
Kết Luận
Bài viết đã cung cấp cho các em học sinh cẩm nang đầy đủ về công thức hình học lớp 9. Hy vọng với những kiến thức được trang bị, các em sẽ tự tin và vững bước hơn trong hành trình chinh phục kỳ thi vào 10 sắp tới. Chúc các em học tập tốt và đạt kết quả cao!
FAQs – Giải Đáp Thắc Mắc Về Công Thức Hình Học Lớp 9
1. Làm sao để nhớ hết tất cả công thức hình học lớp 9?
Có rất nhiều công thức, tuy nhiên bạn không cần phải nhớ máy móc. Hãy tập trung vào việc hiểu bản chất của từng công thức, cách chứng minh và vận dụng chúng. Việc luyện tập thường xuyên với các dạng bài tập khác nhau sẽ giúp bạn ghi nhớ công thức một cách tự nhiên.
2. Ngoài việc học thuộc lòng, còn cách nào khác để học tốt hình học không?
Thay vì học thuộc lòng, bạn nên rèn luyện tư duy hình học bằng cách vẽ hình, phân tích đề bài, tìm mối liên hệ giữa các yếu tố trong hình. Việc kết hợp giữa lý thuyết và bài tập thực hành sẽ giúp bạn nắm vững kiến thức một cách hiệu quả.
3. Làm sao để phân biệt được các dạng bài tập hình học lớp 9?
Mỗi dạng bài tập hình học thường có những đặc trưng riêng. Hãy chú ý đến các dữ kiện đề bài cho, yêu cầu của bài toán và các hình vẽ minh họa để nhận biết dạng bài và áp dụng phương pháp giải toán phù hợp.
4. Nên làm gì khi gặp bài tập hình học khó?
Đừng nản chí khi gặp bài tập khó. Hãy bình tĩnh đọc kỹ đề bài, vẽ hình minh họa, phân tích dữ kiện và cố gắng tìm ra mối liên hệ giữa chúng. Nếu vẫn không tìm ra cách giải, bạn có thể tham khảo lời giải từ giáo viên hoặc bạn bè để rút kinh nghiệm cho bản thân.
Tìm hiểu thêm về:
Nếu bạn cần hỗ trợ thêm về kiến thức hoặc cần giải đáp thắc mắc, hãy liên hệ Số Điện Thoại: 0705065516, Email: thptquangtrung@gmail.com Hoặc đến địa chỉ: NB tổ 5/110 KV bình thường b, P, Bình Thủy, Cần Thơ, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
