Gullit Hình Học Không Gian 11 Tìm Giao Tuyến là một trong những chủ đề quan trọng và cũng là thách thức đối với nhiều học sinh. Bài viết này sẽ cung cấp cho bạn những phương pháp hiệu quả để xác định giao tuyến của hai mặt phẳng, mặt phẳng và đường thẳng trong không gian, kèm theo các bài tập minh họa và lời giải chi tiết.
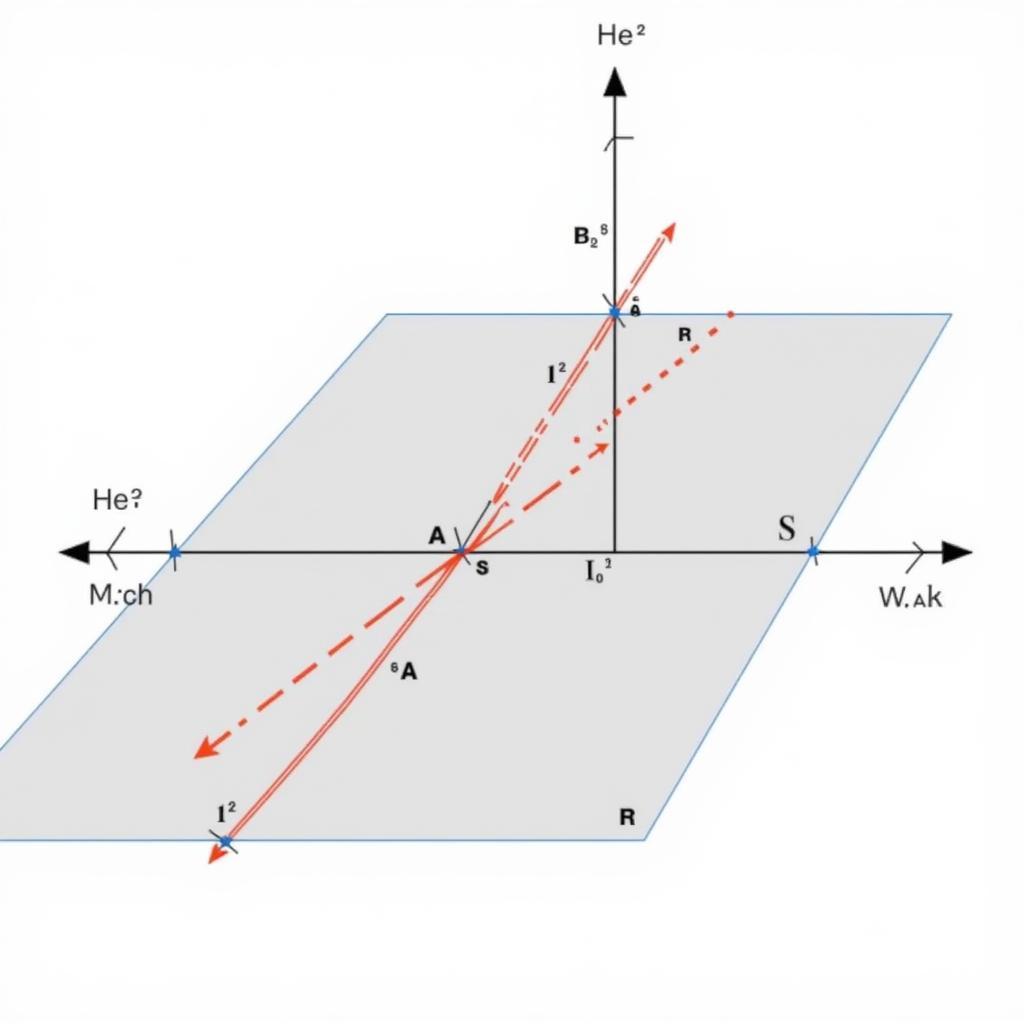Tìm giao tuyến hình học không gian lớp 11
Xác Định Giao Tuyến Của Hai Mặt Phẳng
Để tìm giao tuyến của hai mặt phẳng, chúng ta cần tìm hai điểm chung của hai mặt phẳng đó. Hai điểm chung này sẽ xác định một đường thẳng, chính là giao tuyến cần tìm. Có hai trường hợp thường gặp:
-
Trường hợp 1: Hai mặt phẳng đã có sẵn một điểm chung. Ta chỉ cần tìm thêm một điểm chung nữa bằng cách tìm giao điểm của một đường thẳng thuộc mặt phẳng này với mặt phẳng kia.
-
Trường hợp 2: Hai mặt phẳng không có điểm chung nào cho trước. Ta cần tìm hai điểm chung bằng cách tìm giao điểm của hai đường thẳng thuộc mặt phẳng này với mặt phẳng kia.
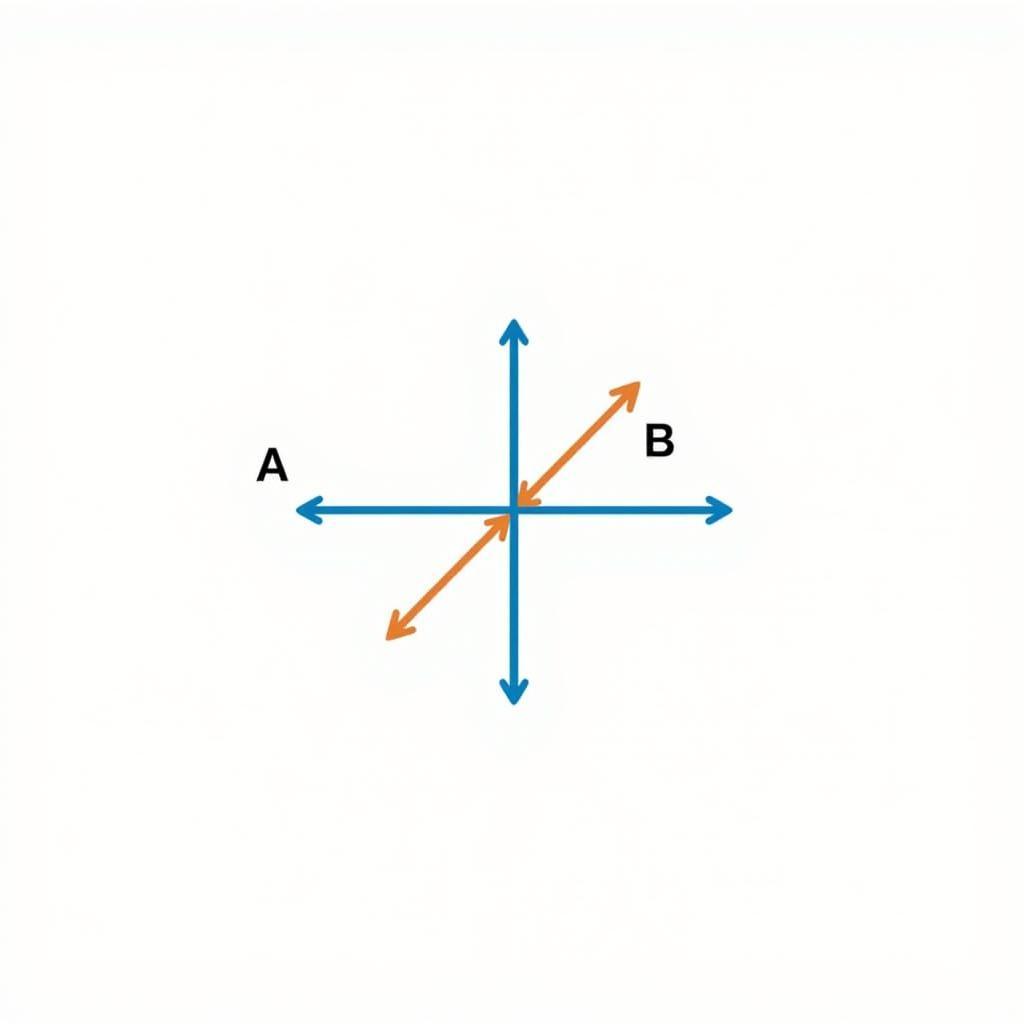Phương pháp tìm giao tuyến của hai mặt phẳng
Ví dụ: Cho hai mặt phẳng (α) và (β). Tìm giao tuyến của (α) và (β). Giả sử ta biết điểm A thuộc cả (α) và (β). Chọn một đường thẳng d nằm trong (α). Tìm giao điểm B của d với (β). Đường thẳng AB chính là giao tuyến của (α) và (β).
Tìm Giao Tuyến Của Mặt Phẳng Và Đường Thẳng
Để tìm giao tuyến của mặt phẳng (P) và đường thẳng d, ta tìm giao điểm của đường thẳng d với mặt phẳng (P). Nếu đường thẳng d nằm trong mặt phẳng (P) thì giao tuyến chính là đường thẳng d.
Các bước tìm giao điểm của đường thẳng và mặt phẳng:
-
Tìm một mặt phẳng (Q) chứa đường thẳng d.
-
Tìm giao tuyến a của mặt phẳng (P) và (Q).
-
Giao điểm của đường thẳng d và đường thẳng a chính là giao điểm của d và (P).
Bạn đang tìm kiếm cách học hiệu quả? Hãy xem bài viết về cách học flashcard hiệu quả.
Bài Tập Vận Dụng Hình Học Không Gian 11 Tìm Giao Tuyến
Bài tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
Lời giải:
- Giao điểm của AC và BD là O.
- S là điểm chung của (SAC) và (SBD).
- Vậy SO là giao tuyến của (SAC) và (SBD).
Bài tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao điểm của đường thẳng SD và mặt phẳng (ABC).
Lời giải:
- Tìm một mặt phẳng chứa SD: (SBD)
- Tìm giao tuyến của (ABC) và (SBD): BD là giao tuyến.
- Tìm giao điểm của SD và BD: D.
- Vậy D là giao điểm của SD và (ABC).
Có lẽ bạn cũng quan tâm đến học 3d.
Kết Luận
Việc nắm vững các phương pháp tìm giao tuyến trong hình học không gian 11 tìm giao tuyến là rất quan trọng để giải quyết các bài toán phức tạp hơn. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và những bài tập thực hành bổ ích.
FAQ
- Làm thế nào để tìm giao tuyến của hai mặt phẳng?
- Cách tìm giao điểm của đường thẳng và mặt phẳng?
- Hình học không gian 11 tìm giao tuyến có những dạng bài tập nào?
- Làm sao để học tốt hình học không gian?
- Có tài liệu nào hỗ trợ học hình học không gian 11 không?
- Ứng dụng của hình học không gian trong thực tiễn là gì?
- Tìm giao tuyến có khó không?
Biết thêm về các trường đại học? Tham khảo các trường đại học nằm ở thủ đức.
Các tình huống thường gặp
- Khó khăn trong việc hình dung không gian ba chiều.
- Nhầm lẫn giữa các phương pháp tìm giao tuyến.
- Không xác định được điểm chung của hai mặt phẳng.
Gợi ý các câu hỏi khác
- Bài tập nâng cao về tìm giao tuyến.
- Phương pháp giải các bài toán hình học không gian phức tạp.
Bạn muốn nâng cao kỹ năng tiếng Anh? Đọc thêm về cách học tiếng anh online.
Cần hỗ trợ thêm về hình học không gian? Hãy liên hệ Số Điện Thoại: 0705065516, Email: [email protected] Hoặc đến địa chỉ: NB tổ 5/110 KV bình thường b, P, Bình Thủy, Cần Thơ, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7. cơ học ứng dụng phần bài tập cũng là một chủ đề thú vị bạn có thể tìm hiểu thêm.
