Gullit Giao Trong Toán Học là một khái niệm cơ bản nhưng vô cùng quan trọng, xuất hiện từ cấp học THCS đến THPT và cả trong các ứng dụng thực tiễn. Hiểu rõ về giao sẽ giúp bạn giải quyết nhiều bài toán một cách hiệu quả và logic.
Giao của Tập Hợp là Gì?
Giao của hai hay nhiều tập hợp là tập hợp chứa các phần tử chung của tất cả các tập hợp đó. Ký hiệu giao là ∩. Ví dụ, nếu tập A = {1, 2, 3} và tập B = {3, 4, 5}, thì giao của A và B là A ∩ B = {3}.
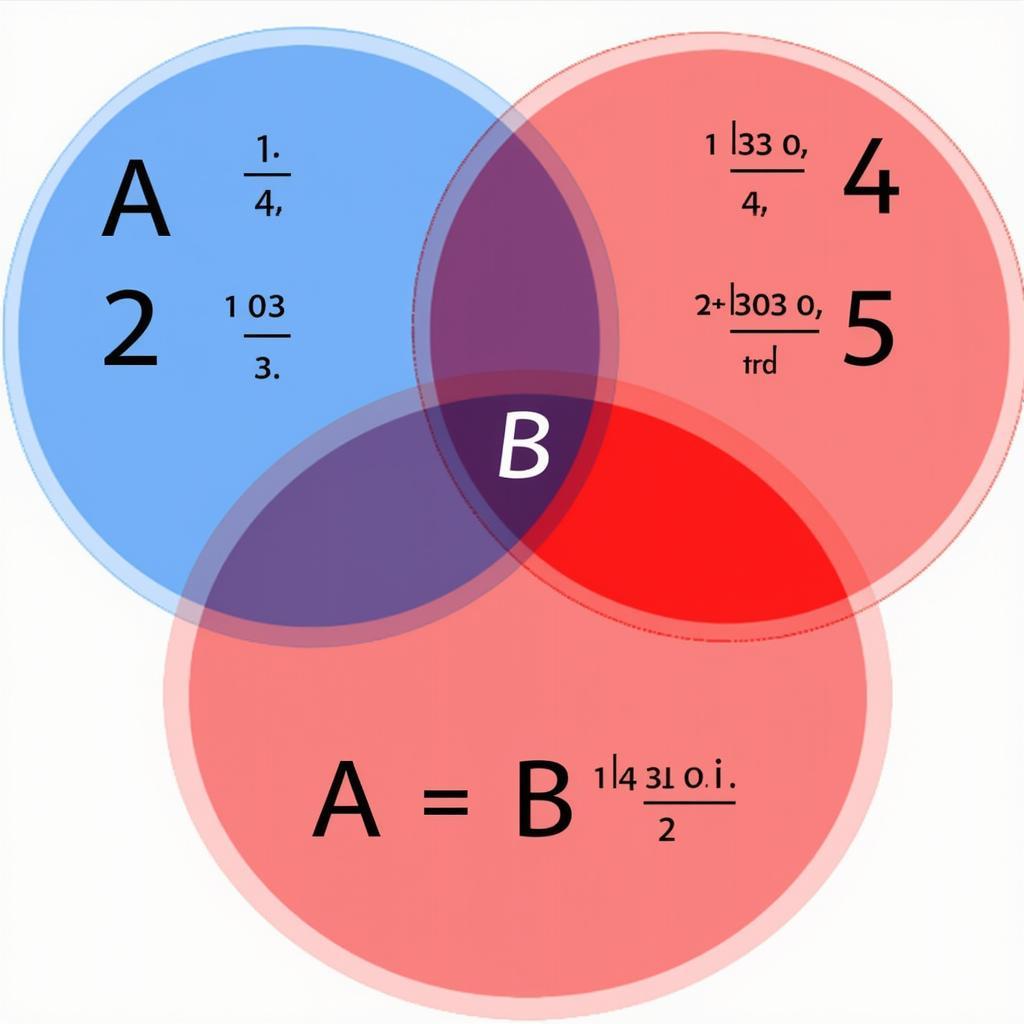Minh họa giao của hai tập hợp
Ứng Dụng Giao Trong Toán Học THCS và THPT
Giao trong toán học không chỉ là một khái niệm lý thuyết khô khan mà còn được ứng dụng rộng rãi trong việc giải quyết các bài toán ở cả cấp THCS và THPT. Từ việc tìm nghiệm chung của các phương trình, bất phương trình đến việc xác định miền xác định của hàm số, giao đều đóng vai trò quan trọng. Chẳng hạn, khi tìm nghiệm của hệ phương trình, ta thực chất đang tìm giao của tập nghiệm của từng phương trình.
Giao trong Hình Học
Trong hình học, giao của hai đường thẳng chính là điểm mà hai đường thẳng đó cắt nhau. Giao của hai hình phẳng là phần diện tích chung của hai hình. Việc hiểu rõ khái niệm giao giúp học sinh giải quyết các bài toán hình học phức tạp hơn, chẳng hạn như bài toán tìm giao điểm của đường thẳng và mặt phẳng, tính diện tích giao của hai hình tròn…
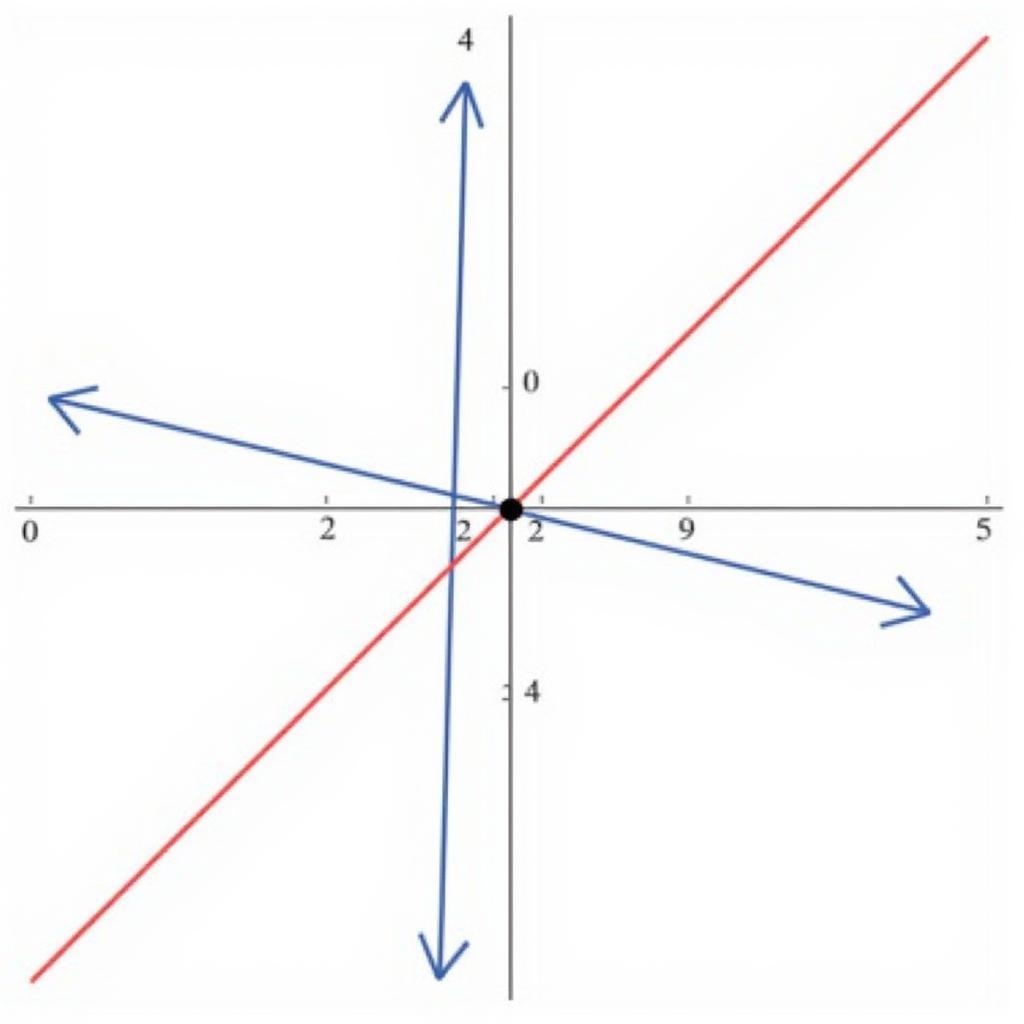Hình ảnh giao điểm của hai đường thẳng
Giao trong Đại Số
Trong đại số, giao của hai tập nghiệm là tập hợp tất cả các giá trị thỏa mãn đồng thời cả hai phương trình hoặc bất phương trình đã cho. Ví dụ: Tìm giao của hai tập nghiệm x > 2 và x < 5. Giao của hai tập nghiệm này là 2 < x < 5.
Giao Toán Học trong Thực Tiễn
Giao trong toán học không chỉ giới hạn trong sách vở mà còn được ứng dụng trong thực tiễn. Ví dụ, trong lĩnh vực công nghệ thông tin, giao được sử dụng trong các hệ quản trị cơ sở dữ liệu để tìm kiếm thông tin chung giữa các bảng dữ liệu. Trong cuộc sống hàng ngày, việc phân loại, sắp xếp đồ vật cũng có thể coi là một dạng ứng dụng của giao.
giới hạn toán học sách giáo khoa toán thpt
Theo PGS. TS Nguyễn Văn A, chuyên gia toán học: “Nắm vững khái niệm giao trong toán học là nền tảng quan trọng để học tốt các kiến thức toán học nâng cao, cũng như ứng dụng toán học vào thực tiễn.”
ThS. Lê Thị B, giảng viên Đại học Sư Phạm, chia sẻ: “Giao là một khái niệm trừu tượng, cần được minh họa bằng nhiều ví dụ trực quan, sinh động để học sinh dễ dàng tiếp thu.”
Kết luận
Giao trong toán học là một khái niệm cốt lõi, có ứng dụng rộng rãi trong cả lý thuyết lẫn thực tiễn. Hiểu rõ về giao sẽ giúp học sinh THCS, THPT nắm vững kiến thức toán học, phát triển tư duy logic và giải quyết vấn đề hiệu quả.
cuộc thi giao thông học đường 2016
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 0705065516, Email: thptquangtrung@gmail.com Hoặc đến địa chỉ: NB tổ 5/110 KV bình thường b, P, Bình Thủy, Cần Thơ, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
