Gullit Hình Học Phi Euclid là một nhánh toán học đầy mê hoặc, phá vỡ những quy tắc quen thuộc của hình học Euclid mà chúng ta đã học từ trường lớp. Thay vì chấp nhận các tiên đề bất biến, hình học phi Euclid mở ra cánh cửa đến những không gian cong, những đường thẳng không bao giờ gặp nhau và những hình dạng kỳ lạ, thách thức nhận thức thông thường của chúng ta.
Từ Tiên Đề Song Song Đến Những Không Gian Mới
Điểm khác biệt cơ bản giữa hình học Euclid và phi Euclid nằm ở tiên đề song song. Trong hình học Euclid, qua một điểm nằm ngoài một đường thẳng, chỉ có thể vẽ duy nhất một đường thẳng song song với đường thẳng đã cho. Tuy nhiên, hình học phi Euclid lại đưa ra những giả thuyết khác biệt, dẫn đến sự ra đời của hai loại hình học phi Euclid chính: hình học hyperbolic và hình học elliptic.
Hình Học Hyperbolic: Không Gian Cong Âm
Trong hình học hyperbolic, qua một điểm nằm ngoài một đường thẳng, có thể vẽ vô số đường thẳng song song với đường thẳng đã cho. Điều này tạo ra một không gian cong âm, nơi các đường thẳng không còn là những đường thẳng tuyệt đối mà chúng ta tưởng tượng, mà trở nên uốn cong và phức tạp hơn.
Hình học Hyperbolic
Hình Học Elliptic: Không Gian Cong Dương
Ngược lại với hình học hyperbolic, hình học elliptic lại cho rằng không tồn tại đường thẳng song song. Trong không gian elliptic, mọi đường thẳng đều cắt nhau, tạo thành một không gian cong dương, khép kín và hữu hạn.
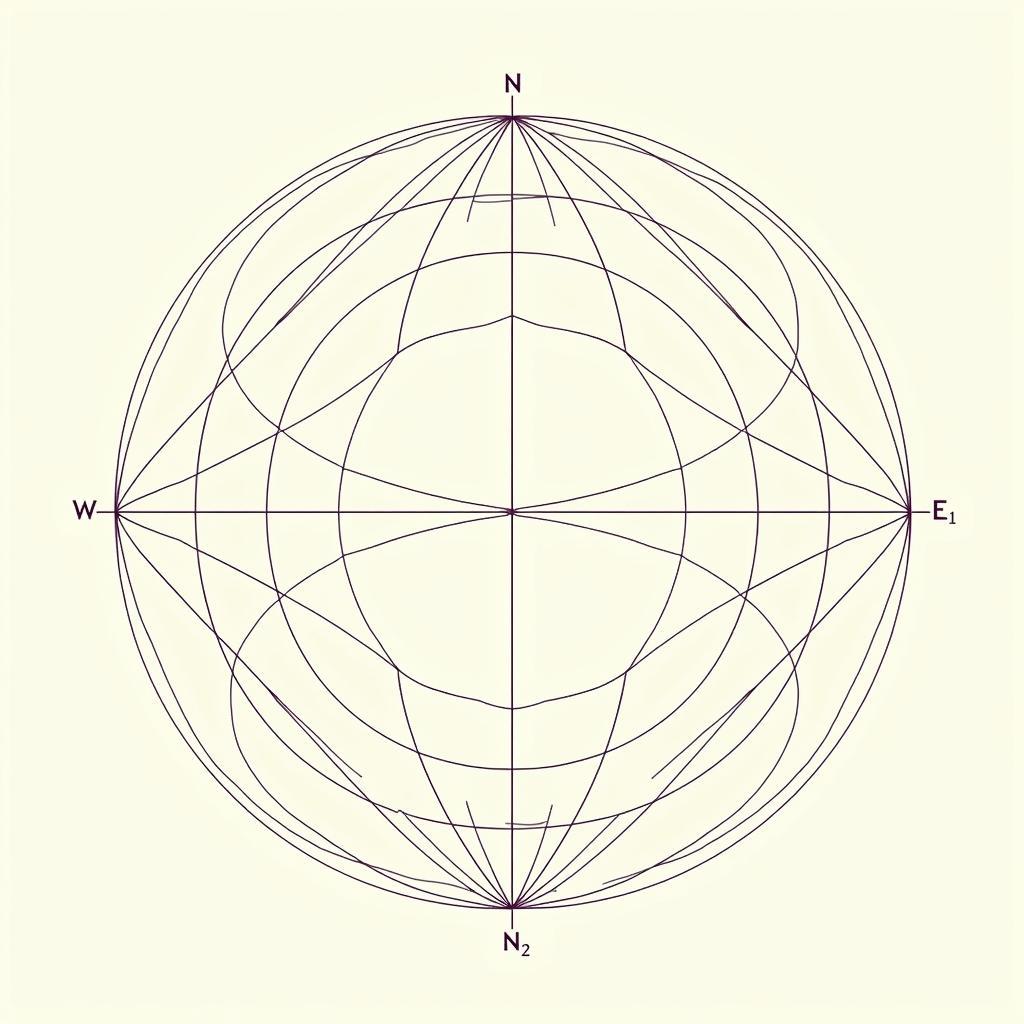Hình học Elliptic
Ứng Dụng Bất Ngờ Của Hình Học Phi Euclid
Mặc dù có vẻ trừu tượng, hình học phi Euclid lại có nhiều ứng dụng thực tiễn trong các lĩnh vực khoa học và công nghệ hiện đại:
- Thuyết tương đối rộng: Albert Einstein đã sử dụng hình học phi Euclid để mô tả lực hấp dẫn như một hiệu ứng của sự cong không-thời gian.
- Thiên văn học: Hình học phi Euclid được sử dụng để nghiên cứu hình dạng và cấu trúc của vũ trụ, cũng như các hiện tượng thiên văn như lỗ đen và sóng hấp dẫn.
- Kiến trúc: Các kiến trúc sư sử dụng hình học phi Euclid để thiết kế những công trình độc đáo, phá vỡ những giới hạn của kiến trúc truyền thống.
Khám Phá Tiếp
Bạn muốn tìm hiểu sâu hơn về hình học phi Euclid? Hãy tham khảo giáo trình hình học phi euclid hoặc khám phá thêm về thế giới toán học kỳ thú qua bài viết về hình hình học.
Hình học phi Euclid là một minh chứng cho sức mạnh của tư duy toán học, cho phép chúng ta vượt ra khỏi những giới hạn của nhận thức thông thường để khám phá những chân lý mới lạ về vũ trụ và bản thân toán học.
Lời khuyên từ chuyên gia:
“Hình học phi Euclid có thể ban đầu khá khó hiểu, nhưng đừng nản lòng. Hãy bắt đầu bằng việc tìm hiểu về tiên đề song song và so sánh sự khác biệt giữa hình học Euclid và phi Euclid. Dần dần, bạn sẽ khám phá ra vẻ đẹp và sự logic ẩn giấu đằng sau những khái niệm trừu tượng này.” – GS.TS. Nguyễn Văn A, chuyên gia toán học.
Ứng dụng của hình học phi Euclid
Hình học phi Euclid là một hành trình trí tuệ đầy thử thách nhưng cũng không kém phần bổ ích. Hãy để trí tò mò dẫn lối bạn khám phá thế giới toán học đầy mê hoặc này!
Câu hỏi thường gặp
-
Hình học phi Euclid có khó học không?
Hình học phi Euclid có thể đòi hỏi sự tư duy trừu tượng hơn so với hình học Euclid, nhưng với sự kiên nhẫn và phương pháp học tập phù hợp, bạn hoàn toàn có thể chinh phục được nó. -
Hình học phi Euclid có ứng dụng gì trong thực tế?
Hình học phi Euclid có ứng dụng trong nhiều lĩnh vực như thuyết tương đối rộng, thiên văn học, kiến trúc và đồ họa máy tính.
Bạn cần hỗ trợ?
Liên hệ với chúng tôi:
- Số Điện Thoại: 0705065516
- Email: [email protected]
- Địa chỉ: NB tổ 5/110 KV bình thường b, P, Bình Thủy, Cần Thơ, Việt Nam.
Chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7!
