Giải Bài Tập Toán Lớp 7 Hình Học Chương 2 tam giác là bước quan trọng giúp học sinh nắm vững kiến thức cơ bản về tam giác, một dạng hình học cơ bản và phổ biến. Chương trình toán lớp 7 hình học chương 2 giới thiệu đến học sinh các khái niệm về góc, cạnh, đường trong tam giác, các loại tam giác, cũng như các định lý quan trọng liên quan đến tam giác như định lý tổng ba góc trong tam giác, bất đẳng thức tam giác…
Tổng Hợp Các Bài Tập Toán Lớp 7 Hình Học Chương 2
Để giúp các em học sinh lớp 7 ôn tập và củng cố kiến thức hình học chương 2 về tam giác một cách hiệu quả, dưới đây là tổng hợp các dạng bài tập thường gặp:
Dạng 1: Nhận Biết Các Loại Tam Giác
- Dựa vào độ dài các cạnh:
- Tam giác đều: Ba cạnh bằng nhau.
- Tam giác cân: Có hai cạnh bằng nhau.
- Tam giác vuông: Có một góc vuông.
- Dựa vào số đo các góc:
- Tam giác nhọn: Có ba góc đều nhọn.
- Tam giác tù: Có một góc tù.
Ví dụ: Cho tam giác ABC có AB = 5cm, BC = 7cm, AC = 5cm. Hãy cho biết tam giác ABC là tam giác gì?
Giải:
Vì tam giác ABC có AB = AC = 5cm nên tam giác ABC là tam giác cân tại A.
Dạng 2: Tính Góc, Cạnh Trong Tam Giác
- Áp dụng định lý tổng ba góc trong tam giác: Tổng ba góc trong một tam giác bằng 180 độ.
- Áp dụng tính chất góc ngoài của tam giác: Số đo góc ngoài của một tam giác bằng tổng số đo hai góc trong không kề với nó.
Ví dụ: Cho tam giác ABC có góc A = 60 độ, góc B = 2 lần góc C. Tính số đo góc B và góc C.
Giải:
Gọi số đo góc C là x (độ). Ta có:
- Góc B = 2x (độ)
- Góc A + góc B + góc C = 180 độ (định lý tổng ba góc trong tam giác)
Thay số ta có: 60 độ + 2x + x = 180 độ
Suy ra: 3x = 120 độ
Vậy: x = 40 độ
Do đó:
- Góc C = 40 độ
- Góc B = 2 * 40 độ = 80 độ
Dạng 3: Chứng Minh Hai Tam Giác Bằng Nhau
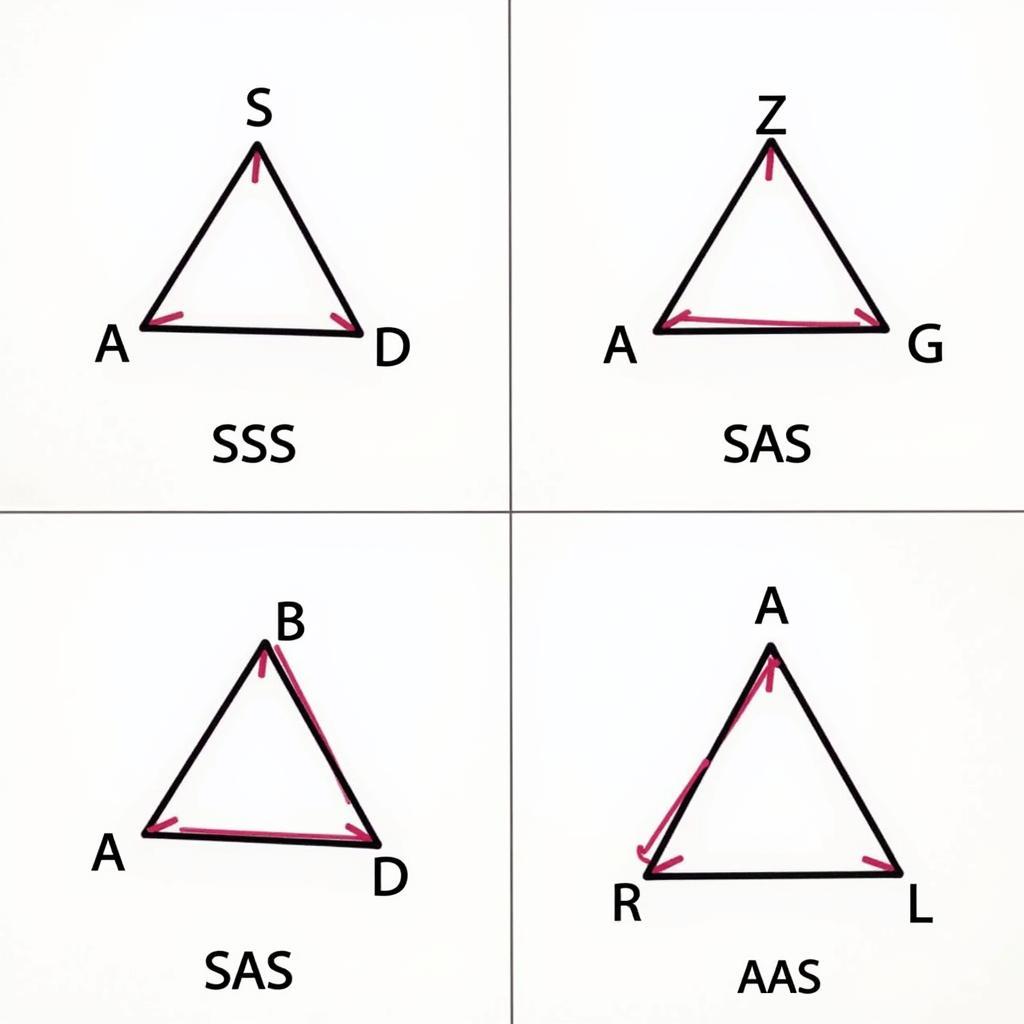 Chứng Minh Hai Tam Giác Bằng Nhau
Chứng Minh Hai Tam Giác Bằng Nhau
- Sử dụng các trường hợp bằng nhau của hai tam giác:
- c.c.c: Ba cạnh của tam giác này bằng ba cạnh của tam giác kia.
- c.g.c: Hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia.
- g.c.g: Hai góc và cạnh xen giữa của tam giác này bằng hai góc và cạnh xen giữa của tam giác kia.
Ví dụ: Cho tam giác ABC có AB = AC, góc BAC = 60 độ. Trên tia đối của tia AB lấy điểm D sao cho AD = BC. Chứng minh tam giác ABC bằng tam giác CDA.
Giải:
Xét tam giác ABC và tam giác CDA, ta có:
- AB = CD (giả thiết)
- AC = CA (cạnh chung)
- Góc BAC = góc DCA = 60 độ (giả thiết)
Vậy, theo trường hợp bằng nhau c.g.c, ta có tam giác ABC bằng tam giác CDA.
Mẹo Giải Bài Tập Hình Học Hiệu Quả
Để giải bài tập hình học hiệu quả, học sinh có thể áp dụng một số mẹo sau:
- Vẽ hình cẩn thận: Hình vẽ chính xác giúp bạn hình dung bài toán rõ ràng hơn và dễ dàng tìm ra cách giải.
- Ghi nhớ các định lý, tính chất: Việc nắm vững lý thuyết là điều kiện tiên quyết để giải quyết mọi bài tập.
- Phân tích đề bài: Xác định rõ yêu cầu của bài toán, từ đó tìm ra hướng giải quyết phù hợp.
- Tìm kiếm các mối liên hệ: Quan sát hình vẽ, tìm kiếm các mối liên hệ giữa các góc, cạnh, đường trong hình.
- Luyện tập thường xuyên: Giải nhiều bài tập từ cơ bản đến nâng cao giúp bạn rèn luyện kỹ năng giải toán và tư duy logic.
Kết Luận
Việc giải bài tập toán lớp 7 hình học chương 2 là một phần quan trọng trong quá trình học tập của học sinh. Hy vọng bài viết này đã cung cấp cho các em những kiến thức bổ ích và phương pháp giải bài tập hiệu quả.
FAQ
Câu hỏi 1: Làm sao để phân biệt tam giác cân và tam giác đều?
Trả lời:
- Tam giác cân: Chỉ cần có hai cạnh bằng nhau.
- Tam giác đều: Có cả ba cạnh bằng nhau và ba góc đều bằng 60 độ.
Câu hỏi 2: Định lý Pitago được áp dụng trong trường hợp nào?
Trả lời: Định lý Pitago chỉ áp dụng cho tam giác vuông: Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Câu hỏi 3: Khi nào nên sử dụng trường hợp bằng nhau c.g.c?
Trả lời:
Nên sử dụng trường hợp c.g.c khi bài toán cho biết hai cạnh và góc xen giữa của hai tam giác bằng nhau.
Bạn Cần Hỗ Trợ?
Liên hệ ngay với trường THPT Quang Trung để được tư vấn và hỗ trợ:
- Số Điện Thoại: 0705065516
- Email: thptquangtrung@gmail.com
- Địa chỉ: NB tổ 5/110 KV bình thường b, P, Bình Thủy, Cần Thơ, Việt Nam.
Đội ngũ chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7!
