Gullit Bài 3 Hình học trong chương trình Toán 10 là bước khởi đầu quan trọng, đặt nền móng vững chắc cho các em học sinh trên con đường chinh phục môn Toán ở bậc THPT. Bài viết này sẽ cung cấp cho các em hệ thống kiến thức đầy đủ, chi tiết và các dạng bài tập thường gặp, giúp các em tự tin giải quyết mọi bài toán trong chương trình Toán 10.
Khám Phá Các Khái Niệm Cơ Bản Trong Hình Học 10 Bài 3
Để giải quyết thành thạo các bài tập Toán 10 bài 3 hình học, trước tiên, các em cần nắm vững những khái niệm cơ bản sau:
- Vectơ: là một đoạn thẳng có hướng, được xác định bởi điểm đầu và điểm cuối.
- Độ dài vectơ: là khoảng cách giữa điểm đầu và điểm cuối của vectơ.
- Hai vectơ bằng nhau: là hai vectơ cùng hướng và có cùng độ dài.
- Tổng và hiệu của hai vectơ: được thực hiện theo quy tắc hình bình hành.
- Tích của vectơ với một số: là một vectơ cùng phương với vectơ ban đầu, có độ dài bằng tích của độ dài vectơ ban đầu với giá trị tuyệt đối của số đó.
Phương Pháp Giải Các Dạng Bài Tập Toán 10 Bài 3 Hình Học
Dựa trên những khái niệm cơ bản, chúng ta sẽ cùng nhau đi vào tìm hiểu phương pháp giải các dạng bài tập Toán 10 bài 3 hình học thường gặp:
Dạng 1: Xác định vectơ, độ dài vectơ và chứng minh hai vectơ bằng nhau
Phương pháp chung:
- Sử dụng định nghĩa vectơ, độ dài vectơ và hai vectơ bằng nhau.
- Áp dụng các tính chất của hình học phẳng (tam giác, hình bình hành,…) để chứng minh.
Ví dụ: Cho hình bình hành ABCD. Chứng minh rằng: $overrightarrow{AB}$ = $overrightarrow{DC}$
Lời giải:
Vì ABCD là hình bình hành nên AB // DC và AB = DC. Do đó, $overrightarrow{AB}$ và $overrightarrow{DC}$ cùng hướng và có cùng độ dài. Vậy, $overrightarrow{AB}$ = $overrightarrow{DC}$.
Dạng 2: Tính tổng, hiệu của hai vectơ, tích của vectơ với một số
Phương pháp chung:
- Vận dụng quy tắc hình bình hành để tính tổng, hiệu của hai vectơ.
- Áp dụng định nghĩa tích của vectơ với một số.
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: $overrightarrow{AM}$ = $frac{1}{2}$($overrightarrow{AB}$ + $overrightarrow{AC}$)
Lời giải:
Vì M là trung điểm của BC nên $overrightarrow{BM}$ = $overrightarrow{MC}$. Ta có:
$overrightarrow{AM}$ = $overrightarrow{AB}$ + $overrightarrow{BM}$ = $overrightarrow{AB}$ + $overrightarrow{MC}$
= $overrightarrow{AB}$ + ($overrightarrow{AC}$ - $overrightarrow{AM}$)
= $frac{1}{2}$($overrightarrow{AB}$ + $overrightarrow{AC}$)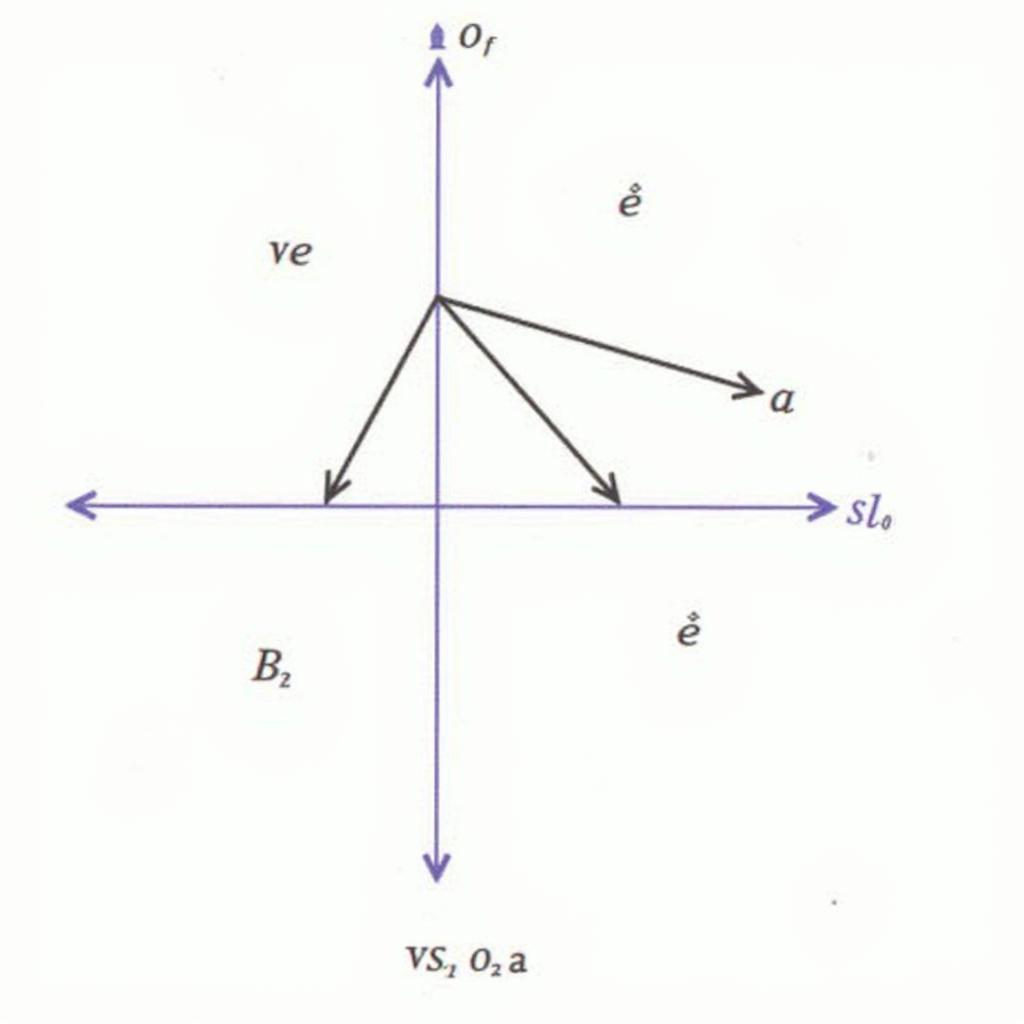
Hình minh họa về vectơ trong bài toán hình học
Dạng 3: Chứng minh ba điểm thẳng hàng, hai đường thẳng song song
Phương pháp chung:
- Để chứng minh ba điểm A, B, C thẳng hàng, ta chứng minh tồn tại số k sao cho $overrightarrow{AB}$ = k$overrightarrow{AC}$.
- Để chứng minh hai đường thẳng AB và CD song song, ta chứng minh $overrightarrow{AB}$ và $overrightarrow{CD}$ cùng phương.
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của AB, N là trung điểm của AC. Chứng minh rằng: MN // BC.
Lời giải:
Ta có:
$overrightarrow{MN}$ = $overrightarrow{AN}$ – $overrightarrow{AM}$ = $frac{1}{2}$($overrightarrow{AC}$ – $overrightarrow{AB}$) = $frac{1}{2}$$overrightarrow{BC}$
Do đó, $overrightarrow{MN}$ cùng phương với $overrightarrow{BC}$. Vậy, MN // BC.
Luyện Tập Giải Bài Tập Toán 10 Bài 3 Hình Học
Để giúp các em củng cố kiến thức và nâng cao kỹ năng giải bài tập, website THPT Quang Trung cung cấp hệ thống bài tập phong phú, đa dạng từ cơ bản đến nâng cao, bám sát chương trình giáo dục phổ thông. Bên cạnh đó, website còn có các video bài giảng trực quan, sinh động giúp các em tiếp thu kiến thức một cách dễ dàng và hiệu quả.
Kết Luận
Bài viết đã cung cấp cho các em những kiến thức trọng tâm và phương pháp giải các dạng bài tập Toán 10 bài 3 hình học. Hy vọng, bài viết này sẽ là tài liệu hữu ích giúp các em tự tin chinh phục môn Toán và đạt kết quả cao trong học tập.
Câu hỏi thường gặp
1. Vectơ là gì?
Trả lời: Vectơ là một đoạn thẳng có hướng, được xác định bởi điểm đầu và điểm cuối.
2. Làm thế nào để tính tổng của hai vectơ?
Trả lời: Ta có thể sử dụng quy tắc hình bình hành để tính tổng của hai vectơ.
3. Khi nào hai vectơ được gọi là bằng nhau?
Trả lời: Hai vectơ được gọi là bằng nhau khi chúng cùng hướng và có cùng độ dài.
4. Tích của vectơ với một số có ý nghĩa gì?
Trả lời: Tích của vectơ $overrightarrow{a}$ khác $overrightarrow{0}$ với một số k là một vectơ cùng phương với $overrightarrow{a}$ và có độ dài bằng $|k|.|overrightarrow{a}|$.
5. Làm thế nào để chứng minh ba điểm thẳng hàng?
Trả lời: Để chứng minh ba điểm A, B, C thẳng hàng, ta chứng minh tồn tại số k sao cho $overrightarrow{AB}$ = k$overrightarrow{AC}$.
Giáo viên đang hướng dẫn học sinh giải bài tập hình học trên bảng
Bạn muốn tìm hiểu thêm về các chủ đề liên quan?
Dưới đây là một số bài viết khác có thể bạn quan tâm:
- Cách học tiếng Anh để thi TOEFL
- Cách học tiếng Anh cơ bản cho người mất gốc
- Học bằng lái xe B2 là gì
Nếu bạn cần hỗ trợ thêm về việc học tập, hãy liên hệ Số Điện Thoại: 0705065516, Email: [email protected] Hoặc đến địa chỉ: NB tổ 5/110 KV bình thường b, P, Bình Thủy, Cần Thơ, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
